A* Search in C++

In this post I want to discuss the a* algorithm (pronounced ‘a-star’), how it is used for motion planning and how we can implement it in cpp.

The process of determining how to get from a start to an endpoint is called ‘planning’ and for a robot it’s called ‘robot motion planning’. There are two broad categories:

discrete motion planning
continuous motion planning

The planning problem is formulated as follows: Given a:

map
starting location
end location
cost function (e.g. shortest, quickest or ‘safest’ path)

Goal: Find the minimum cost path

We can frame the path planning problem as a search problem. Imagine we have the following map:

S    ⛰️    0    0    0    0
0    ⛰️    0    0    0    0
0    ⛰️    0    0    0    0
0    ⛰️    0    0    0    0
0    0     0    0    ⛰️   G

With S(tart) and G(oal) and obstacles in the form of little mountains. Our robot is allowed to travel all points represented by 0 and can only go: up/down, left/right. Our goal is to get from S to G with the minimum number of actions.

Theory

Let’s assume point S has coordinates (0,0). In this case I have only one valid next step: going to point (1,0). Going there costs me one movement point. We will call the sum of the movement points g-value. For every next planned move (every expansion), we start from the point with the smallest g-value. The g-value when the robot hits the Goal is equivalent to the number of steps it has to take in total. This basically amounts to trying every available path, which is not super efficient to put it mildly:)

The a* algorithm comes to the rescue. In order to explore the available options more efficiently, a* uses a heuristic function h(x,y) that measures the distance from a given point (x,y) to the goal, if there were no obstacles present.

The following map shows the h-value for each point on our map:

S    8    7    6    5    4
8    7    6    5    4    3
7    6    5    4    3    2
6    5    4    3    2    1
5    4    3    2    1    G

The actual distance to the goal is therefore always strictly larger or equal to h(x,y): $$ h(x,y) \leq \text{distance to goal from (x,y)} $$

We know keep track of the g-value and of the sum of g-value + heuristic-function value, which we will call f-value. So starting from (0,0) we have (0, 0+9).

So the f-value tells us, how many steps would it take in total, given that it already took a certain number of steps to reach the current point, to get to the goal if there were no obstacles present. So in essence, the f-value is the most optimistic estimate we have to reach our goal, given our current location. Let’s take a look at a concrete example using our map:

Image you are currently at location L. I added the g-value and the heuristic value for our two next possible moves (g, h):

S    ⛰️    0    0    0    0
0    ⛰️    0    0    0    0
0    ⛰️    0    0    0    0
0    ⛰️  (7,4)  0    0    0
0    0     L   (7,2) ⛰️   G

Your g-value at L is 6, the f-value is 9 (6+3). Should we go up or to the right? If we go to the right, we get: (7,7+2) whereas if we go up, we get (7, 7+4). So a* will go right, because we do not want to move away from our goal.

Our a* search algorithm will have the following structure (Credits: udacity.com):

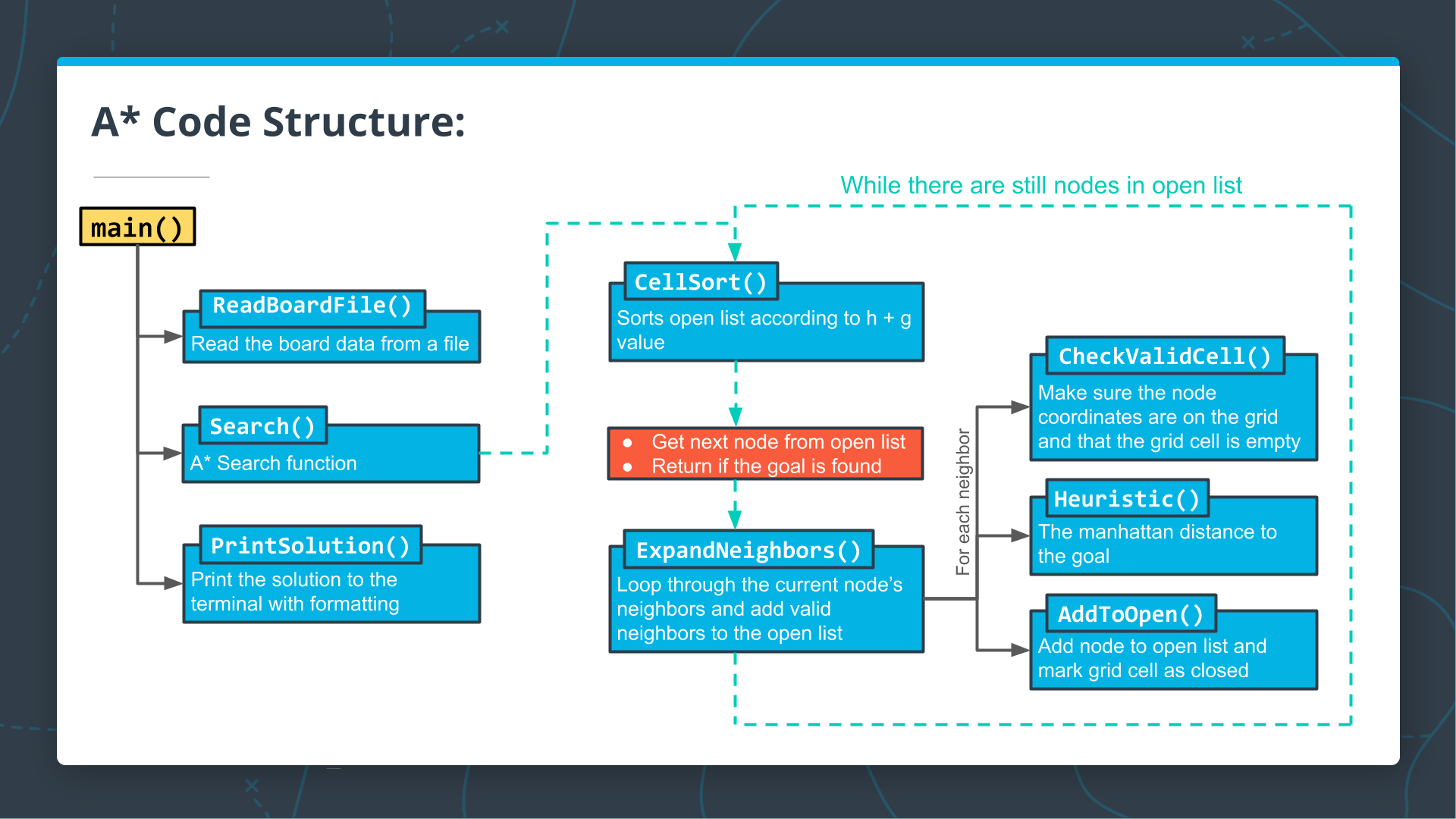
C++ Implementation

Now let’s get going:

#include <iostream>
#include <fstream>
#include <vector>
#include <string>
#include <sstream>
#include <algorithm>

using std::abs;
using std::cout;
using std::istringstream;
using std::sort;
using std::string;
using std::vector;

enum class State
{
    kEmpty,
    kObstacle,
    kClosed,
    kPath,
    kStart,
    kFinish
};

vector<State> ParseLine(string string)
{
    istringstream string_stream(string);
    char c;
    int n;
    vector<State> output;
    while (string_stream >> n >> c && c == ',')
    {
        if (n == 1)
        {
            output.push_back(State::kObstacle);
        }
        else
        {
            output.push_back(State::kEmpty);
        }
    }

    return output;
}

vector<vector<State>> ReadBoardFile(string path)
{
    std::ifstream board_file(path);
    vector<vector<State>> vec_board;

    if (board_file)
    {
        string line;
        int i = 0;
        while (getline(board_file, line))
        {
            vec_board.push_back(ParseLine(line));
        }
    }

    return vec_board;
}
/*
Compare f-values of two cells.
*/
bool Compare(const vector<int> node1, const vector<int> node2)
{

    bool node1_greater_node2 = (node1[2] + node1[3]) > (node2[2] + node2[3]);

    return node1_greater_node2;
}

/*
Sort the two-dimensional vector of ints in descending order.
*/
void CellSort(vector<vector<int>> *v)
{
    sort(v->begin(), v->end(), Compare);
}

int Heuristic(int x1, int y1, int x2, int y2)
{
    return abs(x2 - x1) + abs(y2 - y1);
}

bool CheckValidCell(int x, int y, vector<vector<State>> &grid)
{

    //Check point is on grid
    bool isOnGrid = (0 <= x) && (grid[0].size()) && (0 <= y) && (y <= grid.size());
    //Check if point is empty if on grid
    if (isOnGrid)
    {
        return (grid[x][y] == State::kEmpty);
    }
    return false;
}

void AddToOpen(int x, int y, int g, int h,
               vector<vector<int>> &open_nodes,
               vector<vector<State>> &grid)
{

    vector<int> node{x, y, g, h};

    open_nodes.push_back(node);
    grid[x][y] = State::kClosed;
}

void ExpandNeighbors(
    const vector<int> &current_node,
    int goal[2],
    vector<vector<int>> &open_nodes,
    vector<vector<State>> &grid)
{
    int x = current_node[0];
    int y = current_node[1];
    int g = current_node[2];

    vector<vector<int>> possibleMovements{{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    for (vector<int> movement : possibleMovements)
    {
        int x_test = x + movement[0];
        int y_test = y + movement[1];
        if (CheckValidCell(x_test, y_test, grid))
        {
            int g_test = g + 1;
            int h = Heuristic(x_test, y_test, goal[0], goal[1]);
            AddToOpen(x_test, y_test, g_test, h, open_nodes, grid);
        }
    }
}

vector<vector<State>> Search(
    vector<vector<State>> grid,
    int init[2],
    int goal[2])
{

    vector<vector<int>> open_nodes{};

    int x = init[0];
    int y = init[1];
    int g = 0;
    int h = Heuristic(x, y, goal[0], goal[1]);
    AddToOpen(x, y, g, h, open_nodes, grid);

    while (open_nodes.size() > 0)
    {
        CellSort(&open_nodes);
        vector<int> current_node = open_nodes.back();

        open_nodes.pop_back(); // remove last element from vector
        x = current_node[0];
        y = current_node[1];
        grid[x][y] = State::kPath;

        if (x == goal[0] && y == goal[1])
        {
            return grid;
        }
        ExpandNeighbors(current_node, goal, open_nodes, grid);
    }

    // We've run out of new nodes to explore and haven't found a path.
    cout << "No path found!"
         << "\n";
    return std::vector<vector<State>>{};
}

string CellString(State state)
{
    switch (state)
    {
    case State::kObstacle:
        return "⛰️   ";
    case State::kPath:
        return "🚗   ";
    case State::kStart:
        return "🚦   ";
    case State::kFinish:
        return "🏁   ";
    default:
        return "0   ";
    }
}

void PrintBoard(vector<vector<State>> board)
{
    //alternatively use `auto`
    for (vector<State> v : board)
    {
        for (State i : v)
        {
            cout << CellString(i) << " ";
        }
        cout << "\n";
    }
}

int main()
{
    int init[2]{0, 0}; //int-array
    int goal[2]{4, 5};

    vector<vector<State>> vec_board = ReadBoardFile("1.board");
    vector<vector<State>> solution = Search(vec_board, init, goal);
    PrintBoard(solution);
    return 0;
}

And now we get:

🚗    ⛰️    0    0    0    0
🚗    ⛰️    0    0    0    0
🚗    ⛰️    0    0    0    0
🚗    ⛰️    0   🚗    🚗
🚗    🚗    🚗  🚗    ⛰️  🚗

That is it :)

semper quaerere

A* Search in C++

Theory

C++ Implementation